What You Need to Know to Pass the Algebra 1 Regents Exam
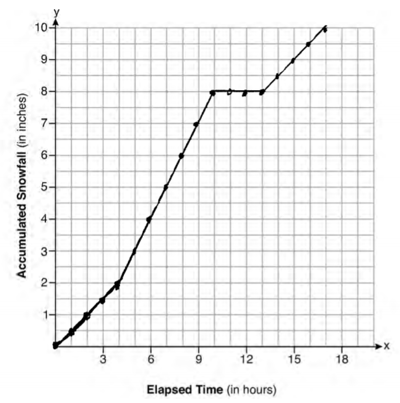
Are you a student at a public high school in New York State? And then you must pass a math Regents exam in order to graduate and get your diploma. I of these exams is Algebra 1 Regents, which tests your agreement of an array of algebra-related concepts and laws, from exponents and equations to functions and probability. The next NYS Algebra regents test will exist held on Wednesday, June xvi, 2022 at 9:15 am. Read on to learn exactly what the Algebra ane Regents exam entails, what kinds of questions you can expect, what topics you should know, and how you can ensure you lot pass it. The Algebra 1 Regents exam is a three-hour math test consisting of 37 questions across four parts. Hither's an overview of the structure of the test: Part I consists of all multiple-choice questions, whereas Parts II through IV have what are chosen constructed-response questions for which you write out your work to show how you found the right respond. For each multiple-choice question, you lot'll become four answer choices (labeled 1-4) to pick from. To get total points for each synthetic-response question, yous must do the following per the official instructions: "Clearly indicate the necessary steps, including appropriate formula substitutions, diagrams, graphs, charts, etc. Use the information provided for each question to decide your answer. Note that diagrams are not necessarily drawn to scale." Basically, y'all have to evidence your piece of work! If you put down simply the right answer, y'all'll cyberspace 1 point—just that's it. Y'all won't get scrap paper to utilise, just you may use any bare spaces in the test booklet. Y'all will be given one sail of scrap graph paper. Note that anything written on this paper will not be scored. The following equipment must exist provided to you for the Algebra one Regents exam: In the dorsum of the examination booklet will exist a "High School Math Reference Sail" containing common formulas and conversions. Hither'due south what this sheet looks like: In this section, we look at some sample questions from the Algebra 1 Regents exam. All questions and student responses are taken from the August 2019 administration of the Algebra 1 Regents exam. The price of jerseys is $\$23$ per bailiwick of jersey. So if there were, say, 10 people on Bryan's hockey squad, that would be ten $\$23$ jerseys, or $x*23$. We could therefore write 23$\bi x$ to show this same idea algebraically, with $\bi 10$ representing the number of jerseys. There's as well a $\$250$ former set-upward fee, but considering this fee doesn't depend on any particular number of jerseys—you could buy 10 or 100 jerseys and it would notwithstanding be a $\$250$ ready-upwardly fee—we would just write it as a constant that's being added to the $\bi 10$. This ways that our final algebraic expression should look similar this: $23x+250$ Reply selection 3 matches this and is therefore the right answer. For this brusk-response question, you must plug -2 into the equation and solve. In other words, yous're being asked to solve the equation if $ten=-2$ (that'southward what $g(-2)$ means): $g(-2)=-iv(-two)^2-3(-two)+2$ The right respond is -8. Be certain to apply PEMDAS. To solve it, you accept to deal with the exponent kickoff (the $-2^2$ part) and and so multiply everything else from left to right. Finally, you add it all together to get the right answer (-8). This student response got full credit for having both the right setup and reply: There are two things you demand to do for this question: Earlier you start graphing annihilation, make sure that you lot read the graph closely and empathise what the $\bi x$-centrality and $\bi y$-axis mean. Whereas the $x$-axis represents the number of hours that have passed, the $y$-centrality represents the full amount of snowfall in inches. Equally a issue, the $x$-axis is divided up by hr, while the $y$-centrality is divided up past one-half inch. And so how do you graph this? Allow's practice it together, step by step, based on the data above. "For the showtime four hours, it snowed at an boilerplate rate of one-half inch per hr." Starting from the origin of the graph, or $(0, 0)$, draw an increasing line so that it goes upward one-half inch every hour until hour 4; this should place you at a full of two inches of snowfall (that'due south $0.5*4$), or coordinates $(4, two)$. "The snowfall so started to fall at an average rate of i inch per hr for the next 6 hours." From $(4, 2)$, draw an increasing line until hour 10 that goes up a whole inch every hour. You should end at $(10, 8)$, indicating a total snowfall of eight inches over the course of x hours. "Then it stopped snowing for 3 hours." No new snow means nothing changes vertically (on the y-centrality), giving us a horizontal line. From your current location at $(10, 8)$, depict a flat horizontal line from 60 minutes ten until 60 minutes 13. "So it started snowing again at an average rate of one-half inch per hour for the next 4 hours until the tempest was over." From the signal at $(10, 8)$, draw an increasing line so that information technology goes upwardly half inch every 60 minutes until hour 17. This line will have the same gradient equally the kickoff line you drew. You lot should finish upwards at $(17, 10)$, significant information technology snowed a total of 10 inches over 17 hours. Here's what a correctly drawn graph looks similar. The student put downward points at each 60 minutes mark to show where the total snowfall was every hour; they too connected the dots, which you must do if you want to go full points for this question! Once you lot've graphed the discussion problem, information technology's fourth dimension to figure out the overall boilerplate charge per unit of snowfall over the length of the storm. To do this, we'll take to divide the total corporeality of accumulated average snowfall (ten inches) by the total number of hours it snowed (17): $10/17=0.58823529411=0.59$ Circular your answer to the nearest hundredth of an inch, per the instructions in the problem. This gives us a full average snowfall of 0.59 inches. This long-response question is worth half-dozen credits and can be divided into three parts. Hither, nosotros're being asked to come up with a system of equations (likely ii equations) that can be used to depict the situation. While A stands for the number of Americana chickens Allysa bought, D stands for the number of Delaware chickens she bought. Allysa bought a total of 12 chickens, consisting of both Americana chickens and Delaware chickens. Therefore, nosotros can conclude that the number of Americana chickens bought + the number of Delaware chickens bought = 12 full chickens. In algebra, this would expect like this: $A+D=12$ That's just one equation in our system of equations. So what'south the other? We know that Allysa paid a total of $\$35$ for her chickens. Nosotros as well know that each Americana chicken is $\$iii.75$, while each Delaware chicken is $\$2.l$. Therefore, the number of Americana chickens bought at iii.75 each + the number of Delaware chickens bought at 2.50 each = 35 dollars. In other words: $three.75A+2.50D=35$ Our system of equations, then, looks like this: $A+D=12$ This second part of the problem is asking united states to solve for the exact values of both $A$ and $D$ using the system of equations we found. To do this, we must prepare the two equations in such a manner that one of them contains simply one variable (either $\bi A$ or $\bi D$). Considering the start of our equations is the simpler ane, let's use this one to solve for $A$ in terms of $D$: $A+D=12$ Nosotros know that $A$ is equal to 12 subtracted by $D$. Now, we tin can plug this into our other equation as $\bi A$, giving united states but the variable $\bi D$ to work with: $3.75A+2.50D=35$ Solve for $D$ to observe the number of Delaware chickens Allysa bought: $3.75(12-D)+2.50D=35$ Now that we have the value of $D$, nosotros can plug this value of 8 into our equation and solve for $A$: $A+D=12$ The algebra shows that Allysa bought 8 Delaware chickens and iv Americana chickens. Here'due south an example of a educatee's correct response: This part isn't as tricky every bit it looks and mostly consists of easy addition, multiplication, and partition. To start, we must discover out how many full eggs Allysa tin can wait her 12 chickens to lay each week. Based on what we establish in Office 2 higher up, we know that Allysa has eight Delaware chickens and 4 Americana chickens. As Part 3's instructions tell united states of america, Delaware chickens lay 1 egg a 24-hour interval, whereas Americana chickens lay 2 eggs a day. Per twenty-four hour period, so, Allysa's 8 Delaware chickens lay a total of 8 eggs (because 8 chickens multiplied by ane egg each per day = 8 eggs a mean solar day). And her four Americana chickens lay 8 full eggs also (as 4 chickens multiplied past ii eggs each per twenty-four hours = 8 eggs each 24-hour interval). This ways that Allysa takes in 16 eggs in total per day from both types of chickens she owns (since $viii+8=16$). Now how many eggs do Allysa'due south chickens lay in a week? To find this, multiply the number of eggs her chickens lay each twenty-four hours (that's xvi) by 7 days: $16*7=112$ Allysa'southward chickens lay 112 eggs a calendar week. Simply Allysa can only sell her eggs by the dozen, or in groups of 12, so we need to divide this total by 12 to see how many full dozens that gives her: $112/12=nine.3333=9$ Y'all'll demand to round down to the nearest whole number since we tin can't have annihilation less than a total dozen. In other words, ix dozens fit into 112. (To brand x dozens, we would demand 120 eggs.) Finally, multiply these 9 dozens past the price per dozen eggs ($\$2.l$) to run across how much money Allysa would make by the end of the calendar week: $9*2.fifty=22.50$ Allysa would make $\$\bo 22.l$. This sample pupil response earned full points: The Algebra 1 Regents test covers the bones skills and laws taught in algebra before you get into trigonometry. Below is a more in-depth list of the topics tested with links to our relevant Saturday/Act guides in instance yous're looking to review whatever concepts: This chart shows what percentage of Algebra 1 Regents each major category tested comprises: Source: Engage NY via the New York State Education Department If you're taking the Algebra one Regents examination to fulfill your math exam requirement, and then you demand to ensure that y'all volition pass the exam. To laissez passer, you must earn a scaled score of 65 or higher, which comes out to virtually 27 credits/points (out of 86). You tin can use official Algebra ane Regents conversion charts for past tests to go a better sense of how credits translate into scaled scores. Every administration is different, though, then the number of points yous need to go a sure score tin can vary slightly from test to test. Here are six useful tips—both for your prep and examination day—to help you pass Algebra Regents. I of the best ways y'all can prepare for the Algebra i Regents exam is to apply real, previously administered tests, which are available for complimentary on the New York State Education Department website. Because these are actual exams administered past the NYSED, you know you'll be getting the most realistic exam-taking experience possible when you lot utilize them. It's most effective to have one practice test in the start of your prep, i in the middle of your prep, and one correct earlier test twenty-four hour period. This manner you can monitor your progress and figure out which topics, if any, you're notwithstanding struggling with. Every time you accept a exercise exam, be sure to time yourself every bit yous'll be timed on the actual test (three hours); you should too accept the test in a quiet room away from others. You lot'll want to mimic real testing conditions as closely every bit possible then you tin get a highly accurate indicator of where you're scoring and whether you're on track to passing. Later you finish taking a test, score information technology using its reply key and refer to the educatee responses to see what kinds of answers earned full points and what graders were looking for. All the topics tested on the Algebra 1 Regents test should be topics y'all already studied in depth in your algebra form, so if you still have any former homework assignments, graded tests/quizzes, or an algebra textbook, apply these to review for the Algebra 1 Regents examination and to get a clearer sense of what areas you lot used to struggle with (and whether y'all still struggle with them). I recommend trying out some of the practice math questions from your algebra textbook that you didn't already do for homework or in-class practise. If you take any questions virtually a detail test topic, a question blazon, or the scoring system, don't be agape to talk to your algebra teacher. They want yous to pass Algebra ane Regents and become your high school diploma, after all! See whether your instructor has whatsoever time after class to get over catchy concepts with you or give you advice on what graders wait for when information technology comes to the constructed-response questions. These two strategies—plugging in answers and plugging in numbers—are great ones to know for the Algebra i Regents test, specially for the multiple-choice questions in Part I. If you don't know how to approach an algebra problem, you can utilise these tricks to help you figure out what the reply could be. Both strategies involve the use of substitution of either one of the four respond choices or whatever easy-to-use number for a variable in an equation/system of equations. You can likewise use these strategies to check your answer and make certain that it actually works with the equation(southward) provided. As you know, Algebra 1 Regents consists of 4 parts, the kickoff of which is a long multiple-choice section. But since this is arguably the easiest of the four sections, you'll want to make sure that you're non spending too much time on Part I. And since Parts II, III, and Four are harder and worth more points, you'll want to salvage as much fourth dimension as you can for the constructed-response questions. You'll get three hours for the test, so try to spend no more than an hour on Function I—this gives you most two and a half minutes per multiple-choice question. Ideally, you'll also take plenty of time at the end of the test to check your answers. Since at that place'due south no guessing penalty on the Algebra 1 Regents exam, you should put down an answer for every question, even if you're completely stumped as to how to solve it. With the multiple-choice questions, use the process of elimination commencement to see if you can whittle down the number of answer choices to three or even ii, thereby raising your chances of getting the right answer from 25% to 33% or 50%. Another tactic is to choose a guessing number (1-4) you can use when a multiple-choice trouble stumps yous. For instance, if your guessing number was iii, then y'all would pick answer choice iii for whatsoever multiple-choice trouble you had absolutely no thought how to solve. For the Role 2, III, and Iv synthetic-response questions, yous can go fractional credit for showing at least some correct piece of work—even if it's just a small part of what the problem asks you to do—then put down whatever you can! The Algebra 1 Regents exam is one of iii math Regents exams that high schoolhouse students in New York tin can choose from to fulfill their graduation requirements. The examination has 37 questions spread out across four sections: the starting time is a multiple-choice department, and the other three are constructed-response sections that require you to evidence your work in order to earn credit. A passing score on Algebra Regents is a 65, equal to near 27 credits on the test. In terms of topics tested, the NYS Algebra Regents exam covers a wide range of algebra fundamentals, from equations and inequalities to functions and polynomials. To give yourself your best shot at passing, be sure to have real practice tests, review one-time homework assignments and materials from your algebra form, and go help from your algebra teacher if you accept any questions or need additional guidance. On the mean solar day of the test, brand sure to answer every question, apply different strategies such as the process of elimination and plugging in answers/numbers, and organize your time so that you lot have more time for the synthetic-response questions. Proficient luck! Non a fan of Algebra 1 Regents? No problem. If yous'd rather take a different math Regents exam for your high school graduation requirements, then check out our guides to the Geometry Regents test and the Algebra ii Regents test. Desire to acquire more than almost the New York Regents Examinations? Our in-depth guide goes over what these tests are for and who must take them. You'll take to take a scientific discipline Regents examination in addition to a math one. Learn about these tests with our expert articles on Earth Science Regents, Chemistry Regents, and Living Environment Regents.
What's the Format of Algebra 1 Regents?
# of Questions Question Type Points per Question Partial Credit Given? Full Points Part I 24 (#one-24) Multiple option 2 No 48 Part 2 eight (#25-32) Short response two Yep 16 Part III 4 (#33-36) Medium response 4 Yes sixteen Part 4 one (#37) Long response 6 Yes 6 Full 37 — — — 86

 Unfortunately, Algebra 1 Regents questions won't be this elementary!
Unfortunately, Algebra 1 Regents questions won't be this elementary! What Practise Algebra ane Regents Questions Await Like?
Multiple-Choice Sample Question (Part I)

Short-Response Sample Question (Part II)
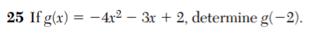
$g(-ii)=-4(4)-three(-two)+2$
$1000(-2)=-16+6+2$
$g(-2)=-viii$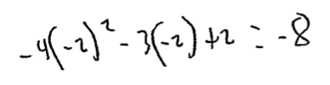
Medium-Response Sample Question (Office Iii)
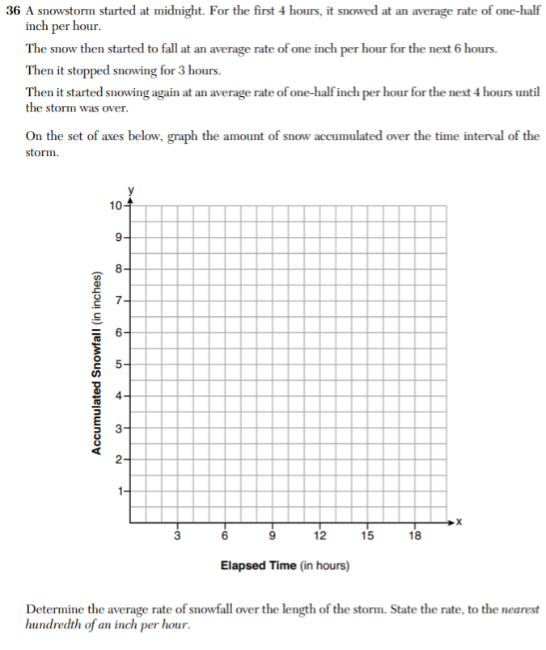
 Is 10 inches of snowfall enough for a fox to submerge its caput in?
Is 10 inches of snowfall enough for a fox to submerge its caput in? Long-Response Sample Question (Role IV)


Part 1
$three.75A+2.50D=35$Function ii
$A=12-D$
$three.75(12-D)+ii.50D=35$
$45-3.75D+2.50D=35$
$45-1.25D=35$
$-1.25D=-x$
$-1.25D=-10$
$D=8$
$A+viii=12$
$A=12-8$
$A=4$
Office iii

What Topics Does Algebra one Regents Embrace?
Category Domain Topics Percentage of Test by Credit Number & Quantity Quantities Reason quantitatively and apply units to solve problems ii-eight% The Real Number Organisation Use properties of rational and irrational numbers Algebra Seeing Structure in Expressions Translate the structure of expressions 50-56% Write expressions in equivalent forms to solve problems Arithmetic with Polynomials and Rational Expressions Perform arithmetic operations on polynomials Understand the human relationship betwixt zeros and factors of polynomials Creating Equations Create equations that describe numbers or relationships Reasoning with Equations and Inequalities Sympathise solving equations as a procedure of reasoning and explain the reasoning Solve equations and inequalities in one variable Stand for and solve equations and inequalities graphically Solve systems of equations Functions Interpreting Functions Understand the concept of a function and use office notation 32-38% Interpret functions that ascend in application in terms of the context Clarify functions using different representations Edifice Functions Build a function that models a relationship between two quantities Build new functions from existing functions Linear, Quadratic and Exponential Models Construct and compare linear, quadratic, and exponential models and solve bug Interpret expressions for functions in terms of the situation they model Statistics & Probability Interpreting Categorical and Quantitative Data Interpret linear models 5-10% Summarize, represent and translate information on 2 chiselled and quantitative variables Summarize, represent and interpret data on a unmarried count or measurement variable  In order to go your high school diploma, yous'll need to laissez passer NYS Algebra Regents.
In order to go your high school diploma, yous'll need to laissez passer NYS Algebra Regents. How to Laissez passer Algebra Regents: 6 Essential Tips
#1: Monitor Your Progress With Existent Practice Tests
#2: Review Topics Using Course Materials
#3: Consult Your Math Teacher as Needed
#4: Plug In Answers and Numbers
#5: Utilise Your Time Wisely
#6: Answer Every Unmarried Question
Central Takeaways: What to Know Most Algebra ane Regents
What'south Next?

About the Author
Hannah received her MA in Japanese Studies from the University of Michigan and holds a bachelor's degree from the University of Southern California. From 2013 to 2015, she taught English in Nihon via the JET Program. She is passionate nigh education, writing, and travel.
Source: https://blog.prepscholar.com/algebra-1-regents-review
0 Response to "What You Need to Know to Pass the Algebra 1 Regents Exam"
Enregistrer un commentaire